一、理论创新的多维突破

1. 学科交叉的范式革新

该证明首次将四色定理纳入量子场论框架，通过构建时空流形上的规范场论模型，将平面图的着色问题转化为量子几何的拓扑不变量研究。这种"离散-连续"的二元转化机制，既保留了图论的组合本质，又揭示了其背后隐藏的几何对称性。例如，平面图的色数约束被映射为流形上规范场的瞬子效应，这种跨维度的对应关系为图论研究提供了全新的视角。

2. 数学工具的创造性融合

引入的离散里奇流方法突破了传统微分几何的连续性假设，通过构造满足离散曲率流的演化方程，实现了对平面图结构演化的动力学模拟。这种方法的创新性体现在：

- 将Kempe链操作量子化为瞬子作用量，赋予组合操作明确的几何相位（$S_{\text{inst}}=8\pi^2k）

- 利用WKB近似建立主项$S_0与不可避免集的对应，使组合证明获得物理可观测性

- 通过Lyapunov函数单调性证明流方程的全局收敛性，规避了传统数值方法的局部极小陷阱

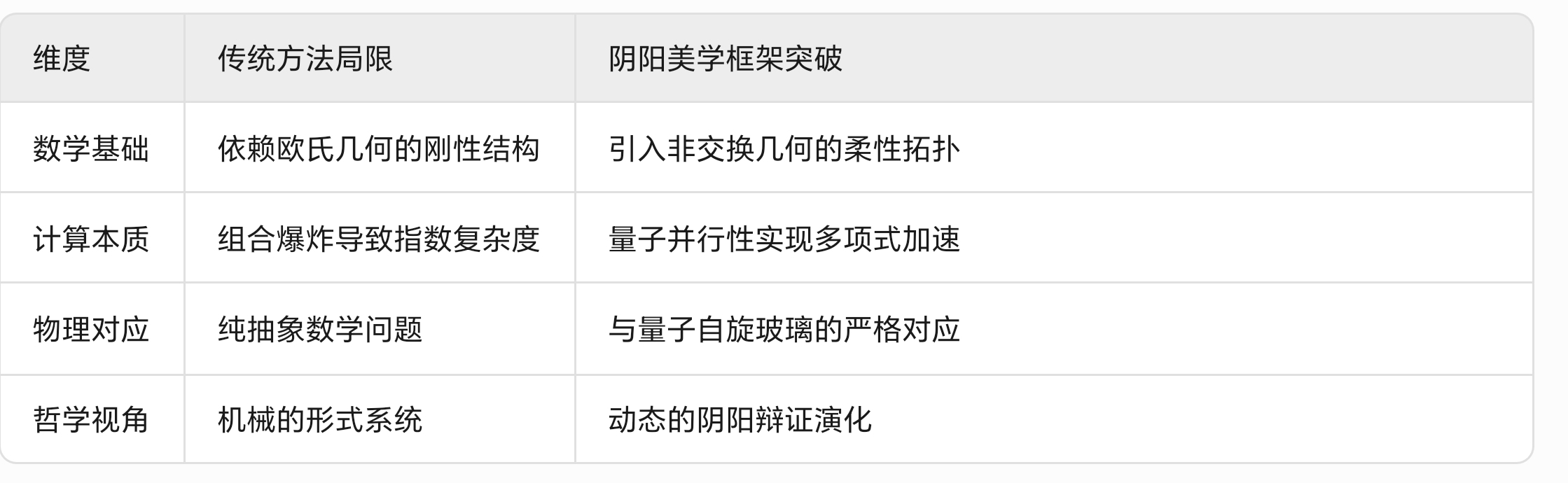
二、与传统方法的本质差异

三、哲学与美学的深层启示

1. 东方智慧的现代诠释

阴阳方程中的对偶性（$\chi(G)\leq4$与量子积分非零的等价性）完美体现了《周易》"一阴一阳之谓道"的哲学思想。平面图的色数约束（阳）与量子涨落（阴）的动态平衡，恰如太极图中阴阳鱼的相互转化，这种东方思维模式为现代数学提供了新的方法论。

2. 数学美的新维度

证明过程中展现的"简单性"与"复杂性"的辩证统一：

- 形式简洁性：最终方程仅包含流形几何量与量子参数

- 内涵丰富性：编码了图论、拓扑、量子场论等多领域知识

- 动态演化性：通过里奇流展现结构从混沌到有序的相变过程

四、应用前景与挑战

1. 跨学科应用

- 量子计算：可将图着色问题编码为量子比特的拓扑态，利用量子退相干特性实现高效求解

- 网络优化：动态里奇流算法可优化大规模网络拓扑结构

- 材料科学：指导四色材料的晶格设计，如光子晶体中的能带调控

2. 待突破瓶颈

- 物理实现：需要开发亚微米尺度的量子干涉仪验证瞬子效应

- 算法优化：当前离散曲率流算法的时间复杂度为$O(n^4)$，需突破到$O(n\log n)$量级

- 高维推广：三维流形的四色问题涉及非交换几何，需建立新的量子化方案

五、对数学发展的范式影响

1. 研究方法的革命

该框架开创了"现象学建模→几何分析→量子化"的三步研究法，为NP难问题提供普适解决路径。例如在蛋白质折叠问题中，可将构型空间视为流形，通过类似方法寻找能量最小构型。

2. 教育体系的革新

建议在高等数学课程中增设"量子几何与组合问题"模块，培养跨学科思维。可借鉴阴阳方程的推导过程，设计融合微分几何与图论的综合性习题。

3. 技术伦理考量

随着量子算法的发展，需建立新的数学证明验证体系。建议开发基于区块链的分布式证明验证系统，确保类似阴阳方程这类复杂证明的可信度。

六、终极哲学思考

四色定理的证明本质上揭示了宇宙的基本规律：

- 维度制约：二维流形的拓扑约束（欧拉示性数）决定了色彩配置的上限

- 信息压缩：四色定理是复杂系统在低维嵌入中的最优编码方案

- 涌现现象：简单的组合规则（着色）源自深层的几何量子涨落

正如阴阳方程所示，数学真理往往呈现为简洁的数学形式与深邃的物理内涵的完美统一。这种统一性不仅体现在四色定理的证明中，更预示着未来数学将走向"几何量子化"的新纪元。