前几天，一位朋友发来消息问道：“按年化收益率5%算，如果我现在开始每月投资2000元，从30岁到60岁能攒下多少钱？要是等到40岁才开始投资，每个月要投资多少钱，才能在60岁时积攒同样的数额？”相信许多正在规划未来的人，心中都藏着类似的疑问。

　　这个问题看似简单，却触及了财务规划的核心——时间与复利的博弈。关于这个问题的答案，与其靠估算猜测，不如用Excel的专业函数来精准计算，既直观又可靠。

　　解答关键：年金终值

　　要解决这个问题，首先得理清其中的关键数据。年化收益率5%是复利计算基础，30岁到60岁有30年时间，每月存2000元属于定期定额投入，在财务计算里叫普通年金；而40岁到60是20年，需要算出在相同目标金额下的月存款额。

　　在财务中，这属于年金终值的计算问题。年金终值指的是在固定期间内，每期等额投资在给定利率下所能积累的总价值。

　　Excel提供了专门的财务函数来处理这类计算，其中FV（未来值）函数用于计算未来价值，PMT函数则用于计算每期投资额，这两个函数都基于复利原理，能够精确量化时间对资金的影响。

　　先来解决第一部分问题：30岁起每月存2000元，年化收益率5%，至60岁的积累总额。这里用FV 函数，它能基于固定利率和等额分期付款，算出投资的未来值。

　　打开Excel并新建一个工作表，找一个空白单元格，比如 A1，在里面输入公式“=FV (5%/12,360,-2000,0,1)”。公式里的参数各有意义，5%/12是把年利率转换成月利率，因为存款是按月进行的；360是总期数，30年共360个月；-2000 代表每月存入的钱，用负数表示资金投入；后面的0，表示初始本金为0元；最后的1表示投资在月初进行，如果是在月末进行投资，这里要把1改成0。输完公式按回车，结果就出来了，约为167.1453万元。

　　没错，30年的坚持和积累，确实可以获得一笔可观的财富，这就是复利被称为“世界第八大奇迹”的原因。

　　再来解决问题的第二部分：如果40岁才开始，只有20年时间，每月需投资多少才能达到相同的167.1453万元？这时候用 PMT 函数，它能计算出为达到某个未来值，每期需要存入的金额。

　　计算方法是：选一个空白单元格，比如B1，输入公式 “=PMT (5%/12,240,0,-1671453,1)”。参数中，5%/12 还是月利率；240是40到60岁的总月数；0表示初始没有本金；-1671453是前面算出的目标金额，用负数是因为在函数逻辑里它是未来要达到的资金；最后一个1同样表示每月投资在期初，如果是期末投资，则要改成0。按下回车，就能得到结果，大约是4050元。

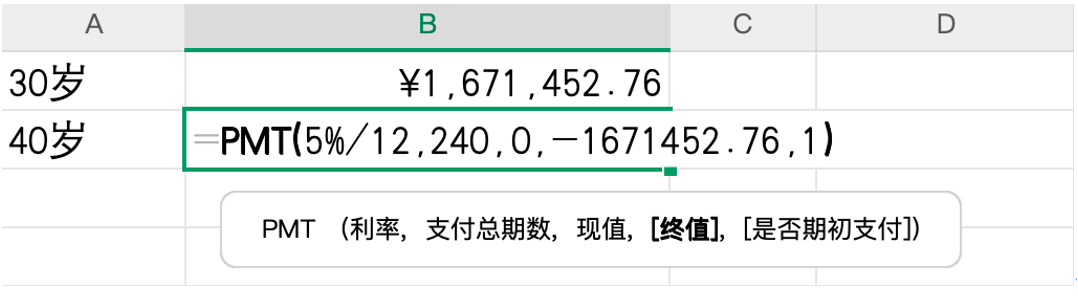
　　两个结果的对比可以看到，在收益率不变的情况下，选择晚投资10年，每月投资的负担增加了1倍多。这个计算直观展示了时间在财富积累中的价值。

　　财务分析的利器

　　掌握这些财务函数的实际价值远超解决单一问题。它们能够帮助我们构建个人财务规划的多种场景分析。例如，教育基金计算：假设18年后需要100万元教育资金，年化收益率为6%，现在需要每月存入多少？同样使用PMT函数即可得出答案。在比较投资产品时，FV 函数能算出不同产品在固定投入下的未来收益，让你一目了然地看出哪个更划算。

　　更进一步，我们可以利用这些函数进行退休规划的综合分析。通过设定不同的收益率、投资额和期限变量，模拟多种情景下的财富积累，找到最适合自己风险偏好和财务能力的投资方案。例如，若能通过投资组合优化将年化收益率从5%提升到6%，最终财富将产生显著差异——这就是资产配置价值的量化体现。

　　大家不妨自己打开Excel亲自试试看吧！